Opady gradu to powszechne zjawisko towarzyszące chmurom Cumulonimbus. Grad dużych rozmiarów jest jednym z głównych czynników niszczących (obok tornad, szkwałów i ulew) w czasie gwałtownych burz.
Spadek ciała w atmosferze
Siły działające na ciało spadające w atmosferze
Aby lepiej zrozumieć istotę gradobić trzeba poświęcić chwilę fizyce związanej z tym zjawiskiem. Po procesie wzrostu w chmurze (który może składać się z wielu cykli) kula gradu wypada poza prąd wstępujący lub osiąga masę, której nie jest w stanie „udźwignąć” prąd wstępujący. Gradzina rozpoczyna proces spadania pod wpływem siły grawitacji. Nie jest to jednak jedyna siła działająca na spadającą kulę gradu (tak byłoby w próżni) – wraz ze wzrostem jej prędkości rośnie skierowana przeciwnie do kierunku spadania siła oporu aerodynamicznego (patrz rysunek). Tylko początkowo ciało spada ruchem jednostajnie przyspieszonym, a wraz ze wzrostem jego prędkości (i wzrostem siły oporu) jego przyspieszenie jest coraz mniejsze. Ciało przyspiesza do momentu, gdy rosnąca siła oporu powietrza zrówna się z siłą grawitacji. Wówczas osiąga ono tzw. prędkość graniczną i dalej porusza się ruchem jednostajnym. W praktyce oznacza to, że skaczący z wysokości kilku kilometrów spadochroniarz tuż przed otwarciem spadochronu osiągnie podobną prędkość do słynnego „człowieka-pająka”, któremu przy wspinaczce na wysokości 300 metrów powinęła się noga. Ta prędkość w dolnej troposferze w przypadku człowieka wynosi od około 200 km/h (ręce i nogi rozłożone) do ponad 300 km/h (ciało zwinięte w kłębek). Felix Baumgartner osiągnął podczas spadania ponad 1300 km/h, co jednak wynikało ze znacznie mniejszej gęstości powietrza w wyższych warstwach atmosfery.
Prędkość spadającej kuli gradu
Na siłę oporu aerodynamicznego, jak można wnioskować z poprzedniego akapitu, wpływ ma samo ciało (kształt i wielkość) oraz jego prędkość spadania, a także gęstość powietrza. Aby obliczyć prędkość i energię spadających kul gradu należy przedstawić pewne wzory:
Wzory sił działających na spadające ciało
Po przyrównaniu do siebie dwóch sił możemy obliczyć prędkość graniczną. Przy założeniu że grad jest kulą lodową otrzymujemy wzór na prędkość graniczną gradziny:
Wzór na prędkość spadającej kuli gradowej
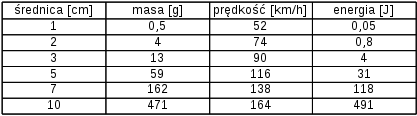
Na podstawie obliczeń widać, że prędkość graniczna, przy niezmienności pozostałych parametrów, rośnie wraz z wielkością kuli gradu (proporcjonalnie do pierwiastka średnicy). A więc wraz ze wzrostem gradziny nie tylko rośnie jej masa, ale również prędkość spadania. Stąd mamy bardzo szybki wzrost energii kinetycznej gradu (proporcjonalny do czwartej potęgi rozmiaru). Oto tabelka z obliczonymi wielkościami fizycznymi dla gradu różnej średnicy:
Masa, prędkość i energia kul gradowych
To tłumaczy dlaczego 1-centymetrowy grad jest na ogół nieszkodliwy, a 2-centymetrowy grad niszczy uprawy podczas gdy grad 7-centymetrowy i większy może już niszczyć dachy i stwarzać śmiertelne zagrożenie dla ludzi. Energia kinetyczna 10-centymetrowej kuli lodowej jest 16 razy większa od energii 5-centymetrowej gradziny i wynosi niemal 500 J – jest to wielkość zbliżona do energii pocisku wystrzelonego z pistoletu kalibru 9 mm. O prędkości i energii niszczącej dużego gradu (do 7 cm) świadczy film z Bisztynka (https://www.youtube.com/watch?v=xKYtz5LvH9Y). Zdecydowanie nie jest to pogoda na spacer.
Obliczenia, a praktyka
Gigantyczny grad
Powyższe obliczenia bazują na uproszczonym modelu rzeczywistości – w praktyce gradziny mogą być bardziej nieregularne, a ich podawany rozmiar to najdłuższa przekątna (a nie średnica). W takiej sytuacji owalny grad wielkości 7 cm może w rzeczywistości posiadać masę kuli o średnicy np. 5 cm. Nieregularny kształt może również zwiększać współczynnik oporu aerodynamicznego. Z powodu wymienionych czynników w praktyce prędkości spadania gradu mogą być o 30 % niższe, a energie kinetyczne nawet kilkukrotnie mniejsze. Im grad masywniejszy i bardziej zbliżony do kształtu kuli, tym jego prędkość i energia powinna być bardziej zbliżona do powyższych obliczeń.
Kolejnym istotnym elementem jest gęstość kuli gradowej, która ze względu na różną budowę warstw gradowych może być nieco mniejsza niż zakładana. W przypadku małego gradu w chłodnej porze roku jego gęstość może być znacznie mniejsza od przyjętej w obliczeniach, co się przekłada na mniejszą prędkość spadania. Innym czynnikiem mogą być interakcje kuli gradowej z innymi hydrometeorami oraz prędkość powietrza, w którym następuje spadek. Jeżeli grad spada w na granicy oddziaływania prądu wstępującego, to jego prędkość końcowa będzie mniejsza. Analogicznie grad spadający w obrębie silnego prądu zstępującego może mieć prędkość większą od teoretycznej. Na zdjęciu powyżej przedstawiono gigantyczną gradzinę osiągającą rozmiar niemal 20 cm. Można sobie wyobrazić, jak ogromną miała energię i jak silne prądy wstępujące posiadała superkomórka burzowa, która stworzyła omawianą kulę gradową.
Prędkość pionowa prądów wstępujących
Bardzo silny prąd wstępujący
Dochodzimy do zagadnienia zbliżonego do wcześniej omawianego: jak silne są prądy wstępujące w chmurze Cumulonimbus powodującej opady dużego gradu? Bierzemy pod uwagę warunki polskie i zakładamy, że grad jest masywną kulą o średnicy 8 cm. Jest to ekstremalna u nas wielkość gradu (zdarzał się w Polsce grad rozmiarów do 10 cm, ale nie były to idealne kule). Okazuje się, że w czasie formowania się gradu w chmurze zachodzą analogiczne procesy jak w czasie jego spadania. Siła grawitacji działa niezmiennie, a siła oporu aerodynamicznego jest wytwarzana przed prąd wstępujący, który „dźwiga” gradzinę w chmurze. Prędkość graniczna takiej gradziny wynosi 147 km/h. Ta wielkość obliczana jednak była dla powietrza przy powierzchni ziemi. Grad formuje się w środkowej troposferze (przy temperaturach -10, -20°C), gdzie gęstość powietrza stanowi około 55% tej przy powierzchni ziemi (poziom 500 hPa, temperatura -10°C). Po uwzględnieniu tej zmiany prędkość prądu wstępującego, który utrzymuje gigantyczny grad w środkowej troposferze wynosi 197 km/h – to ogromna wartość. Coś dla szukających mocnych (i ostatecznych) wrażeń szybowników. Tak mocne i długotrwałe prądy wstępujące występują tylko w ekstremalnie silnych superkomórkach burzowych i jedynie w bardzo sprzyjających warunkach. Istotny jest fakt, że do poziomu 500 hPa wyzwala się zazwyczaj co najwyżej połowa energii konwekcji (CAPE), co oznacza, że w wyższych warstwach troposfery prąd wstępujący może jeszcze przyspieszyć o kilkadziesiąt procent (być może do prędkości znacznie powyżej 250 km/h!). Są to już jednak rozważania teoretyczne, ponieważ prędkość prądu wstępującego w superkomórkach bierze się nie tylko z wyporności (CAPE), ale również z działalności mezocyklonu,
Trudno też o dokładne pomiary prędkości pionowej prądów wstępujących. Teoretyczna, maksymalna prędkość prądów wstępujących w warunkach bardzo dużej chwiejności (CAPE=3000 J/kg) wynosi niemal 280 km/h. W praktyce prędkość ta jest zwykle znacznie mniejsza (przynajmniej o połowę), ale w przypadku superkomórek może być inaczej. Przykładowo wg NOAA do wytworzenia 3-calowego gradu (a więc niewiele mniejszego niż 8 cm) potrzebny jest prąd wstępujący o prędkości 160 km/h, co jest wartością niższą od powyżej obliczonych 197 km/h. Nie jest powiedziane, czy chodzi tu o wartość występującej w środkowej troposferze (strefa tworzenia się gradu), czy w górnej troposferze (teoretycznie największe prędkości prądów pionowych). Możliwe również, że przyjęto inne założenia co do niektórych stałych. Czasem prąd wstępujący jest tak silny, że można to zauważyć wizualnie, gdy chmura „rośnie w oczach”. Tak jak w sytuacji na powyższym zdjęciu chmury, która przyniosła w Białymstoku grad wielkości 4-5 cm.
